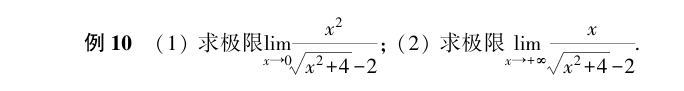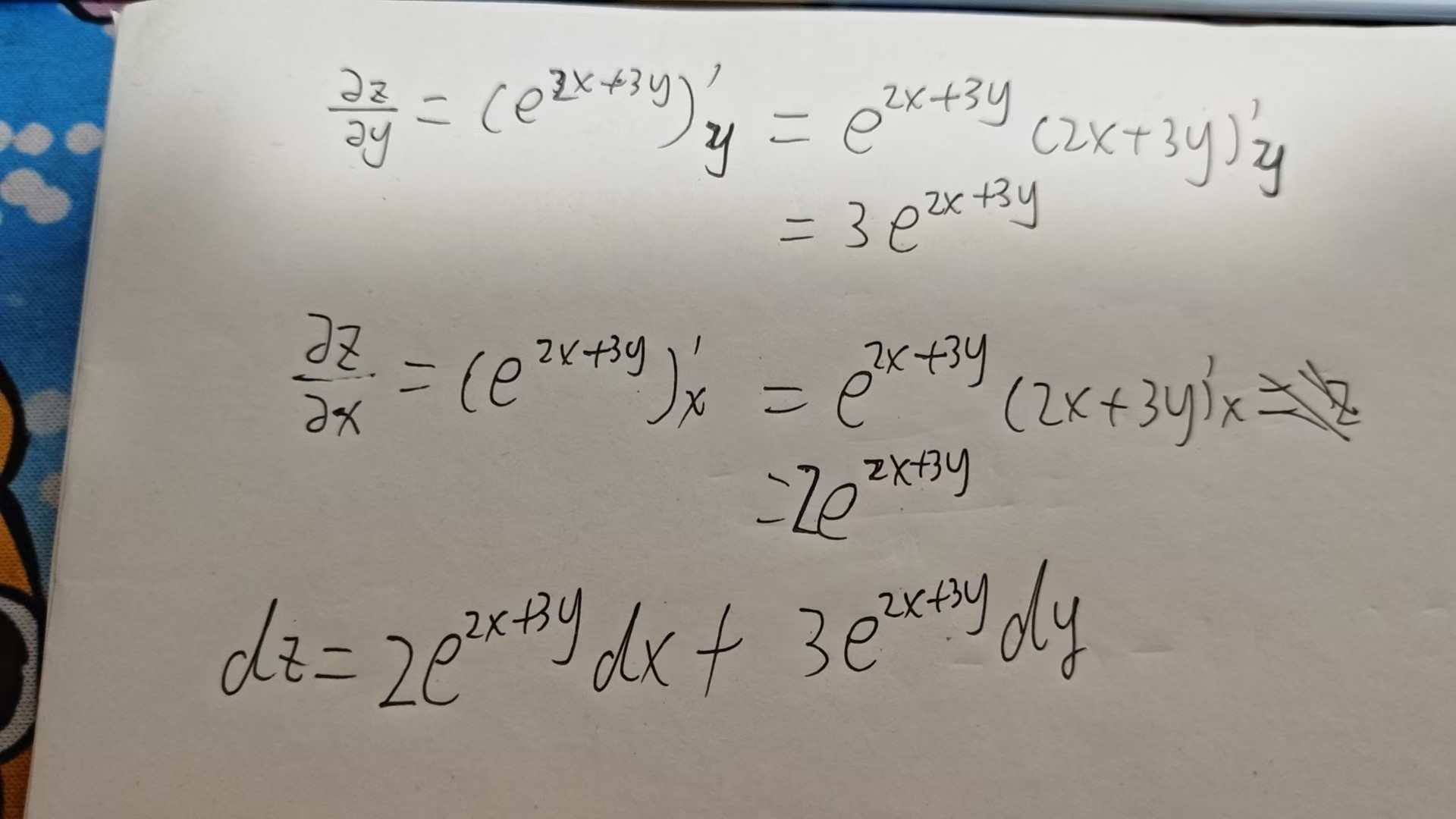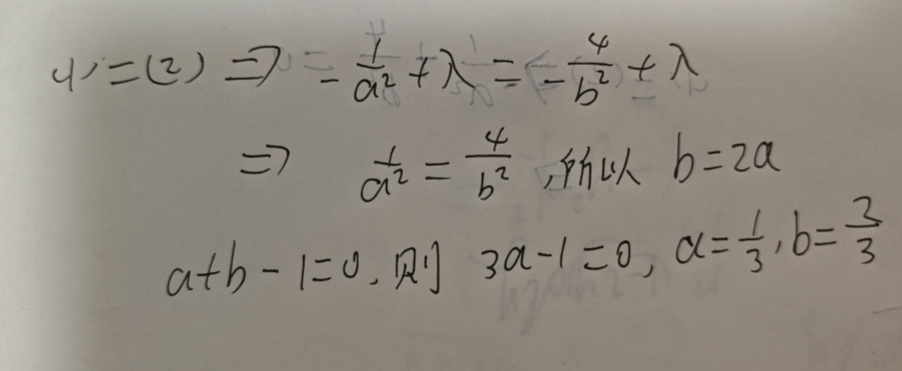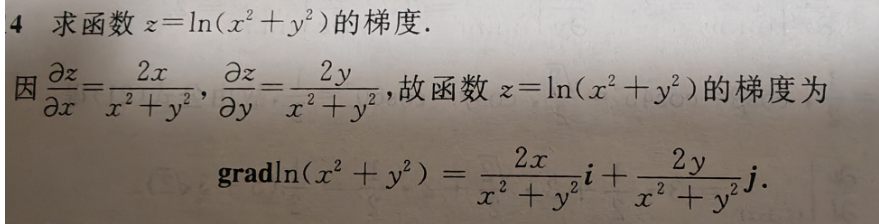微积分
由于学习微积分需要一定的基础知识,但是由于本教程不是数学书,所以不能一一详细介绍基础知识,读者需要自行了解学习初等函数、三角函数等基础知识。
1.1. 极限
极限的符号是 lim ,在高等数学中,主要是数列极限和函数极限,限于篇幅,本文只讨论函数存在极限时的一些情况。
数学上有正无穷大( +∞ )和负无穷大( −∞ )的概念,大家都知道无穷大的意思,但是比较容易理解错无穷小、负无穷大,无穷小指的是无限接近 0,而不是负数的无穷大。
举个例子你就明白了,当 x→+∞ 时, x1 的值,我们都知道 x 越大, x1 越小,但是不可能为 0,只能越来越接近于 0。
求解极限,一般会碰到这几种情况,当 x 无穷大时,y 是多少。
例如下图所示,当 x 无穷大时,y 逐渐贴近 x 轴,即 y 越来越接近,我们使用 y→0 表示趋近于 0 或者说接近 0。
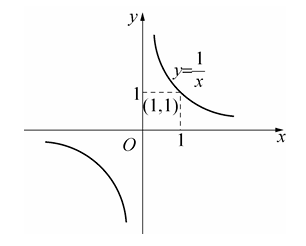
图片来自《高等数学上册》第一章第三节函数极限的定义与计算,同济大学数学系编著。
所以:
x→∞limf(x)=x→∞limx1=0
使用 C# 表示时,我们使用一个极大的数表示无穷大。
var x = torch.tensor(double.MaxValue);
var y = 1 / x;
var lim = (int)y.item<double>();
Console.WriteLine(lim);
上面使用了 y.item<double>() 将张量转换为标量,我们也可以使用函数 y.ToScalar().ToInt32(); 转换。
再比如下图所示,当 x 无穷大时,y 越来越接近 2π ,所以 :
x→+∞limarctanx=2π
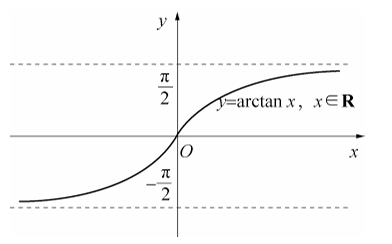
图片来自《高等数学上册》第一章第三节函数极限的定义与计算,同济大学数学系编著。
上面求极限时,是当 limx→∞ 或 limx→0 时的情况,在实际中更多的是给出某点,求其极限,例如:
x→x0limf(x)=x→x0limx1
当 x=1 时,我们直接计算其实可以得到 y=1,极限就是 1,或者换句话来说,我们求一个函数在 x0 的极限时,如果你可以直接计算出 y0 的值,那么这个值就是该点的极限。
这种函数计算极限很简单,因为可以直接通过 y=f(x) 计算出来。
下面这道题是也是同济大学《高等数学上册》中的两道题。
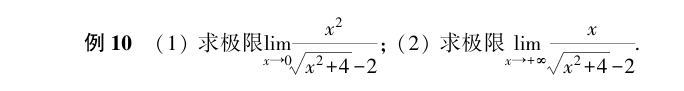
当 x 解决 0 时,分子是 0,0 除以任何数都是 0,所以极限是 0?肯定不是呀。
当碰到这种 x→0 分子或分母为 0 的情况,就不能直接计算了。这两道题的解答过程:

由于本文不是数学教程,因此这里不再深入讨论细节。
在高等数学中,有两种非常重要的极限:
x→0limxsinx=1,x∈(0,2π)
x→0lim(1+x)x1=e
1.2. 导数
给定一个函数,如何计算函数在某个区间上的变化率?
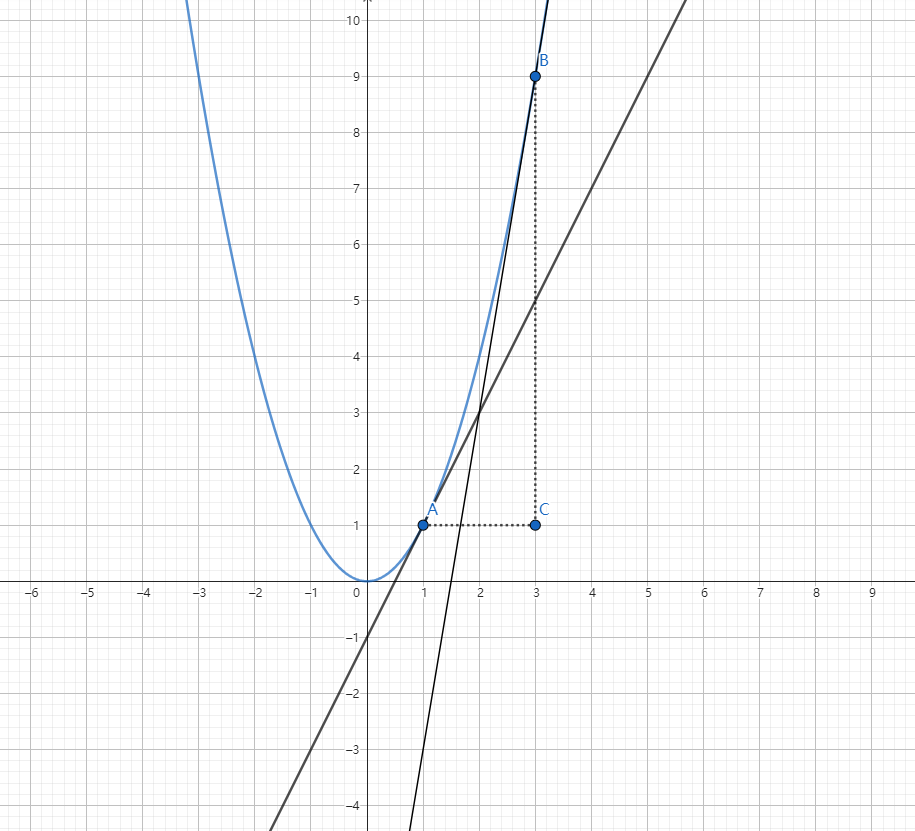
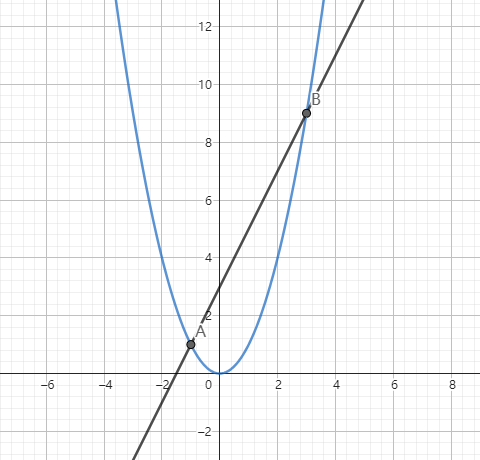
如图所示,函数 y=x2 在区间 [1,3] 的起点 A 和 终点 B。
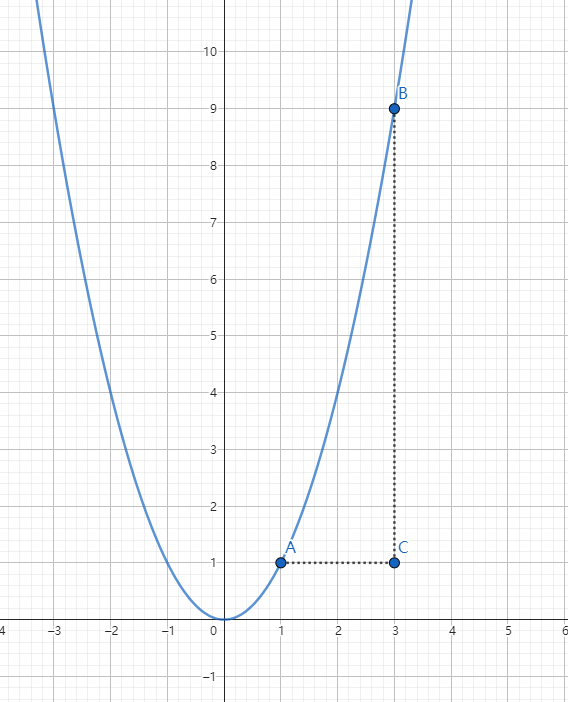
那么平均变化率就是:
△x△y=3−19−1=28=4
但是当这个 △x 或 △y 非常小时,事情就会变得非常复杂。如果我们要求 x=9 附近的平均变化率,则:
x+△xy+△y=3+△x9+△y
当 △x△y 非常小时,实际上反映了函数在 x=9 时的瞬时变化率。那么这个瞬时变化率,我们可以过 A、B 点使用切线表示。
切线是轻轻接触函数一点的一条线,由图可知,当 x 越来越大时, y2=x+1 比 y1=x 大很多,比如 52 、 42 、 32 之间的差,越来越大。
那么切线可以反映这种变化率。如图所示,B 点的切线角度比 A 的的切线大。
因此,出现了一种新的函数,叫原函数的导函数,简称导数,导数也是一个函数,通过导数可以计算原函数任一点的瞬时变化率。
导数的表示符号有多种,例如:
△x△y=f′(x)=y′=dxdy=xdf(x)=xdf
d 是微分符号,例如 dy 是对 y 的微分,dx 是对 x 的微分。
如果要求在某点 x0 的瞬时变化率,则:
△x△yx0=f′(x)x0=y′x0=dxdyx0=xdf(x)x0=xdfx0
读者应该都有一定的数学基础吧,前面两种应该很容易理解,而后面三种也很重要,在积分和微积分的学习中,我们将会大量使用这种方式。
我们可以这样理解:
dy=△y
dx=△x
在 Pytorch 中,我们可以通过微分系统进行计算,例如我们要计算 d(x2)x=3 。
var func = (torch.Tensor x) => x.pow(2);
var x = torch.tensor(3.0, requires_grad: true);
var y = func(x);
y.backward();
var grad = x.grad.ToScalar().ToDouble();
Console.WriteLine(grad);
不要搞错,计算导数后,要使用 x 输出导数值,而不是使用 y,因为 y 是函数结果。为什么求导的时候不直接输出求导结果呢?因为 Pytorch 自动求导系统是非常复杂的,计算的是偏导数,对于一元函数来说,对 x 的偏导数就是 y 的导数,在后面的偏导数和梯度时,会更多介绍这方面的知识。
另外创建 x 的张量类型时,需要添加 requires_grad: true 参数。
求导公式
下面是同济大学《高等数学》中的一些基本求导公式。

例如,我们求 y=x2 的导数,使用上图的 (2)式,得到 y=2x。
对于复合函数和复杂函数的求导会很麻烦,这里不再赘述。对于复杂的函数,还存在高阶导数,即导数的导数,二阶导数公式如下:
f′′(x)=y′′=dx2d2y=x2d2f(x)=x2d2f
乘除求导例题
主要例题有乘法求导、商求导、指数求导几种。
① 求下面函数的导函数。
f(x)=excosx
解:
f′(x)=(excosx)′=(ex)′cosx+ex(cosx)′=excosx−exsinx
求下面函数的导数:
y=lnxx+1
解:
y′=(lnx)2(x+1)′lnx−(x+1)(lnx)′=(lnx)2lnx−(x+1)x1=x(lnx)2xlnx−(x+1)
复合函数求导的链式法则
如果 y=f(u) 在点 u 处可导,u=g(x) 在点 x 出可导,则复合函数 y=f[g(x)] 在点 x 处可导,且有:
dxdy=dudy⋅dxdu
如果函数比较复杂,还可以推广到有限个复合函数的情况,例如:
dxdy=dudy⋅dvdu⋅dxdv
例题,求 y=e2x 的导函数。
设 u=2x ,则:
y′=(eu)′=eu⋅(u)′=e2x⋅(2x)′=2e2x
Sigmoid 函数的导数
经过上面的学习,我们知道由复合函数求导公式可知:
(vu)′=v2u′v˙−uv˙′
所以对于 (f(x)1)′ 此类函数的求导,可得出:
(f(x)1)′=−f(x)2f′(x)
Sigmoid 函数 σ(x) 是神经网络中最有名的激活函数之一,其定义如下:
σ(x)=1+e−x1
在后面学习梯度下降时,需要对 Sigmoid 函数进行求导,使用下面的公式求导会比较方便:
σ′(x)=σ(x)(1−σ(x))
当然,你也可以使用分数的求导方法慢慢推导。
σ′(x)=(1+e−x1)′=1+e−x1−(1+e−x)21=1+e−x1(1−1+e−x1)=σ(x)(1−σ(x))
求最小值问题
函数的斜率有一个性质,当函数的斜率为 0 时,该点 a 取得极值,即 f′(a)=0 ,该点的切线平行于 x 轴。
画出 y=3x4−4x3−12x2+32 的图形如下所示,由图可知分别在 x=−1 、 0 , 2 三个点存在极值,此时斜率都是 0 ,其中当 x=2 时,函数取得最小值,该函数无最大值。
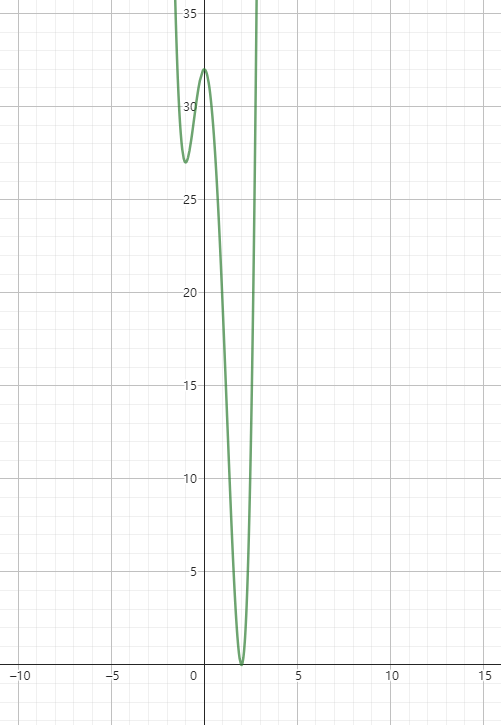
那么如果给定一个函数,我们如果取得这个函数的所有极值和最小最大值?这里可以使用穿针引线法。
首先对函数进行求导并化简。
y′=(3x4−4x3−12x2+32)′=12x3−12x2−24x=12x(x2−x−2)=12x(x+1)(x−2)
由此可知,该函数在 x=−1,0,2 三点的斜率为 0,然后分别计算在这三点的值,做出如下图所示。
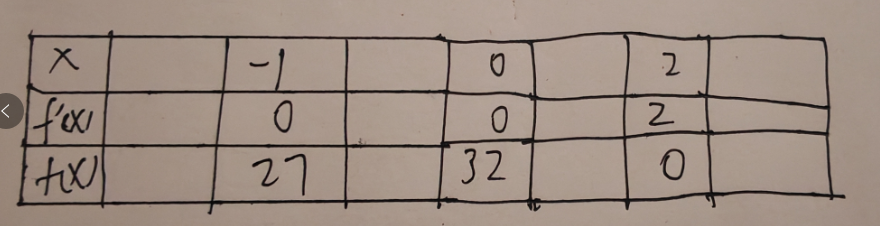
然后计算导数在区间的正负,例如当 x<−1 时,由于导数的结果是负数,所以 f(x) 递减区间。根据导数的正负,确定 f(x) 的递增递减区间,然后作出新的表格。
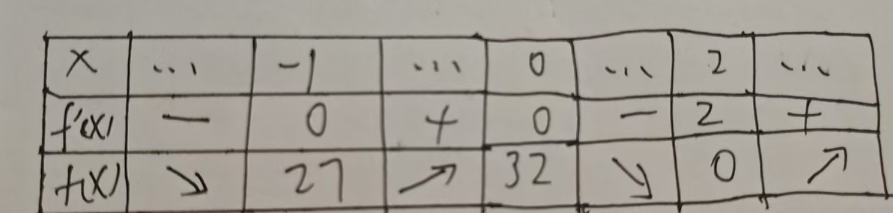
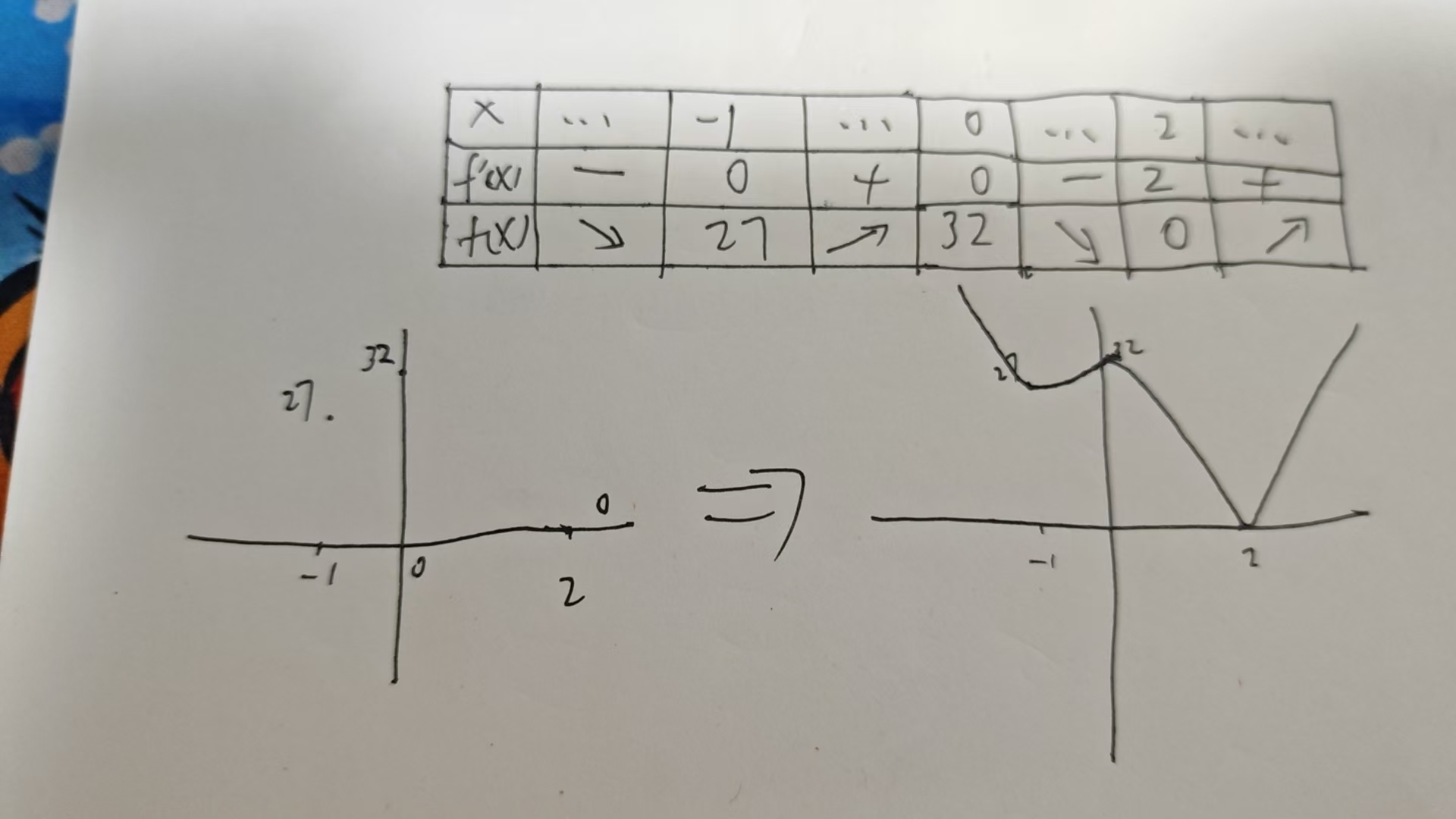
接下来就简单了,根据三个点的值,在坐标轴上描点,最后按照递减区间连线,因此最小值是 0。
手画图不需要准确,主要是知道递增递减区间和极值就行。
1.3. 微分
下面是同济大学《高等数学》中的一张图。
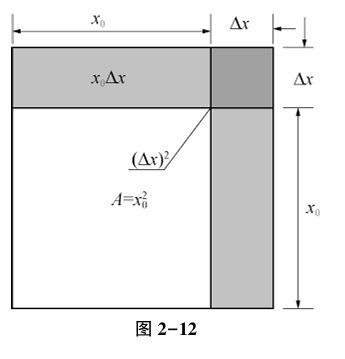
由图可知,在正方形 A 中,其面积是 A=(x0)2 ,而大正方形的面积是 (x0+△x)2 ,或者通过多个矩形面积相加得出大正方形面积为:
S=x02+2x0△x+(△x)2
那么,在边长增加了 △x 的时候,面积增加了多少呢?
△S=2x0△x+(△x)2
我们可以使用下面的公式来表示当 y=f(x) 满足一定关系时,其增量的表达式:
△y=A△x+O(△x)
前面在讲解导数时,我们知道 △y=f(x+△x)−f(x) ,所以:
△y=f(x+△x)−f(x)=A△x+O(△x)
当 △x 非常小时,并且 A=0 时,可以忽略 O(△x) ,我们使用 A△x 近似计算 △y 的值,这就是微分的定义,其中 A=f′(x) 。
dy=f′(x)△x
举个例子,求 y=x3 在 x=1 时, △x=0.01 和 △x=0.001 的增量。
上题本质就是求 x=1.01 和 x=1 时 △y 以及 x=1.001 和 x=1 时 △y 。
先求:
(1.01)3=1.030301
(1.001)3=1.003003001
所以两个增量方便是 0.030301、0.003003001。
但是如果只需要求近似值,那么我们使用微分方式去求,首先求出导数:
y′=dy=(x3)′=3x2
所以:
dy=3x2△x
所以 △x=0.01 时,有:
dy=3∗(1)2∗0.01=3∗0.01=0.03
所以 △x=0.001 时,有:
dy=3∗(1)2∗0.001=3∗0.001=0.003
所以可以这样通过微分 dy 的方式近似计算函数的增量。
因为:
△y=dxdy
我们使用 dy 近似代替 △y ,这就是微分的应用场景之一。
1.4. 积分
前面介绍了导数,我们知道 y=x3 的导数是 y=3x2。
那么反过来,我们知道一个函数 F(x) 的导数是 y=x3 ,对于幂函数,我们很容易反推出 41x4 的导数是 x3 ,但是 41x4+1 、 41x4+666 的导数都是 x3 ,所以 x3 的原函数是不确定的,所以反推得出的积分公式,又叫不定积分,我们使用 C 来表示这个不确定的常数。
假设原函数是 F(x),导数是 f(x) ,由于常数在求导时会被消去,所以求积分时,需要出现加上这个不确定的常数,所以:
∫f(x)dx=F(x)+C
下面是同济大学《高等数学》给出一些积分公式。

前面介绍了微分的作用,这里也给出导数在平面中的简单应用场景。
如图所示,图中的是 y=x2 函数的封闭区域,和 x=0 、 x=2 两个直线围成了一个封闭区域,求 ABC 所围成的封闭区域的面积。
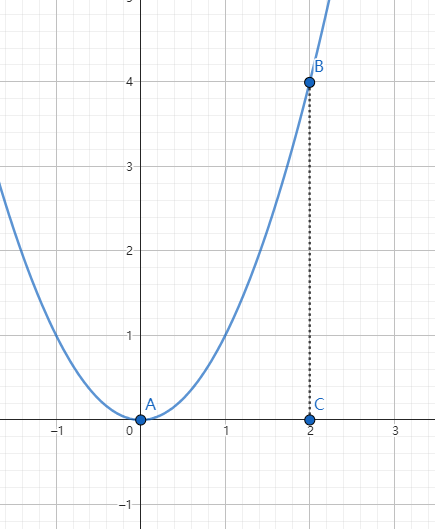
首先求出其原函数为 y=31x3 。使用积分区间表示求解的面积:
∫12x2=31x312=3123−3113=37
对于上面求解的问题,使用的是积分公式,如下公式所示,∫ 表示积分符号, f(x) 表示被积函数, dx 表示积分变量增量(微分), a 和 b 表示积分的下限和上限,即积分区间。
∫abf(x)dx
下面再来一道简单的题目,求 y=2x+3 和 y=x2 所围成的面积。
首先要求得积分区间,即两者的两个交点,由 x2=2x+3 得:
x2−2x−3=0
根据十字相乘法,得:
(x+1)(x−3)=0
所以 x1=−1 , x2=3。
我们先求 y=2x+3 在这两个点之间围成的面积。
∫−132x+3=x2+3x−13=(9+9)−(1−3)=20
求 y=x2 在这两个点所围成的面积。
∫−13x2=31x3−13=9−(−31)=9+31
所以围成的面积是: 20−(9+31)=332 。
在数学上,我们可以更加方便表示这种两个函数加减的方法,即:
∫−13(2x+3−x2)=∫−13(2x+3)−∫−13(x2)
1.5. 偏导数
偏导数属于多元函数的微分学,最常见的是求解空间问题,在初高中基本只涉及一元函数,在这里我们引入二元函数,记作:
z=f(x,y)
在一元函数中,导数是函数沿着 x 轴的变化率,而在多元函数中由于有多个变量,不能直接计算导数,要针对某个轴方向进行求导,所以叫偏导数,接下来,我们将逐渐学习偏导数的一些基础知识。
多元函数定义域
下面给出一个二元函数构成的图形。
z=1−x2−y2
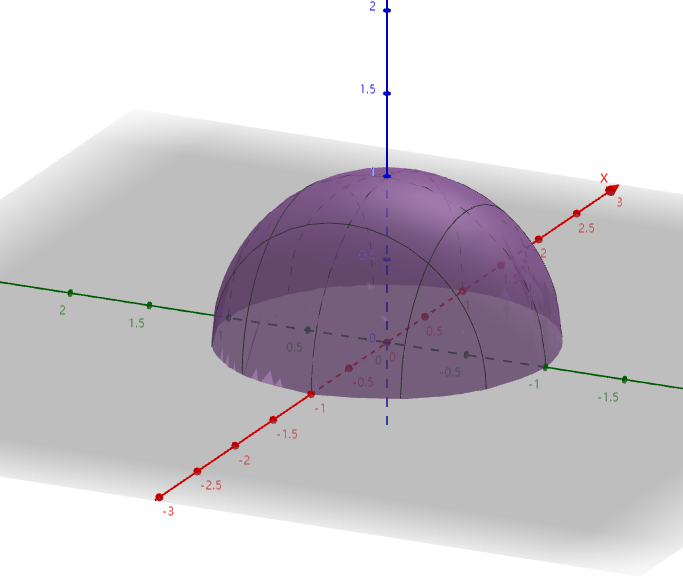
下面提个问题,怎么求这个 z=1−x2−y2 的定义域?
我们知道 1≥x2+y2 ,在设 y=0 时, 1≥x2 ,则 −1≤x≤1 ,由于 1−x2≥y2 ,所以 −1−x2≤y≤1−x2。
所以定义域:
−1≤x≤1−1−x2≤y≤1−x2z≥0
这个函数是二元函数,求定义域还是比较简单的,z 是 f(x,y) 的函数,我们先求出 x 的定义域,然后求出 y 定义域。推广到 u=f(x,y,z) 三元函数,一般 x 定义域是常数,y 的定义域由 x 的函数组成,而 z 的定义域由 x、y 的函数组成。
求解空间中两个立体图形组成的封闭的空间体积时,就是使用定积分去求,计算定积分需要知道定义域,就是这种求法,本文不再赘述。
多元函数的值
已知函数 f(x,y)=x2+y2xy ,求 f(1,2)。
其实也很简单,方便使用 x=1,y=2 替代进去即可:
f(1,2)=12+222=51
多元函数的极限
前面提到极限的时候,涉及到的都是一元函数,对于多元函数的极限,计算则复杂一些,我们可以使用以下公式表示二元函数在某点的极限值。
y⟶y0x⟶x0limf(x,y)=A
求二元函数的极限,称为二重极限。
例如求下面函数的二重极限。
y⟶2x⟶1limln(x+y2)=ln(1+22)=ln5
偏导数
对多元函数求导的时候,由于函数有多个未知变量,例如 z=x2+y2 ,由于里面有 x、y 两个变量,因此函数也就有两个变化方向,求导的时候要设定是往哪个方向,例如要知道往 x 轴方向的变化率,那就是要针对 x 进行求导,求在 z=f(x0,y0) 时 x 的导数,这个就叫对 x 的偏导数。
偏导数使用符号 ∂ 表示,那么对 x 的偏导数可以记作:
∂x∂zy=y0x=x0
当然还有很多变体,Markdown 敲数学公式超级累,这里贴个图省事儿。

下面给个简单函数的偏导数,方法很简单,当对 x 求偏导数时,把 y 当常数处理即可。
z=x2+y2
∂x∂z=2x,∂y∂z=2y
再如:
z=x2+yx+y2
∂x∂z=2x+y,∂y∂z=2y+x
前面提到积分可以求解平面中两个函数所组成的封闭区域的面积,偏导数则可以计算空间中立体几何和平面组成的封闭区域面积,这里就不再深入。
全微分
设二元函数 z=f(x,y) 则其全增量公式为:
△z=A△x+B△y+O(β)
那么关于 z 的微分:
dz=fx(x,y)dx+fy(x,y)dy
求全微分,其实就是先求出所有偏导数,然后再进行计算。
例如求 z=e2x+3y 的全微分。
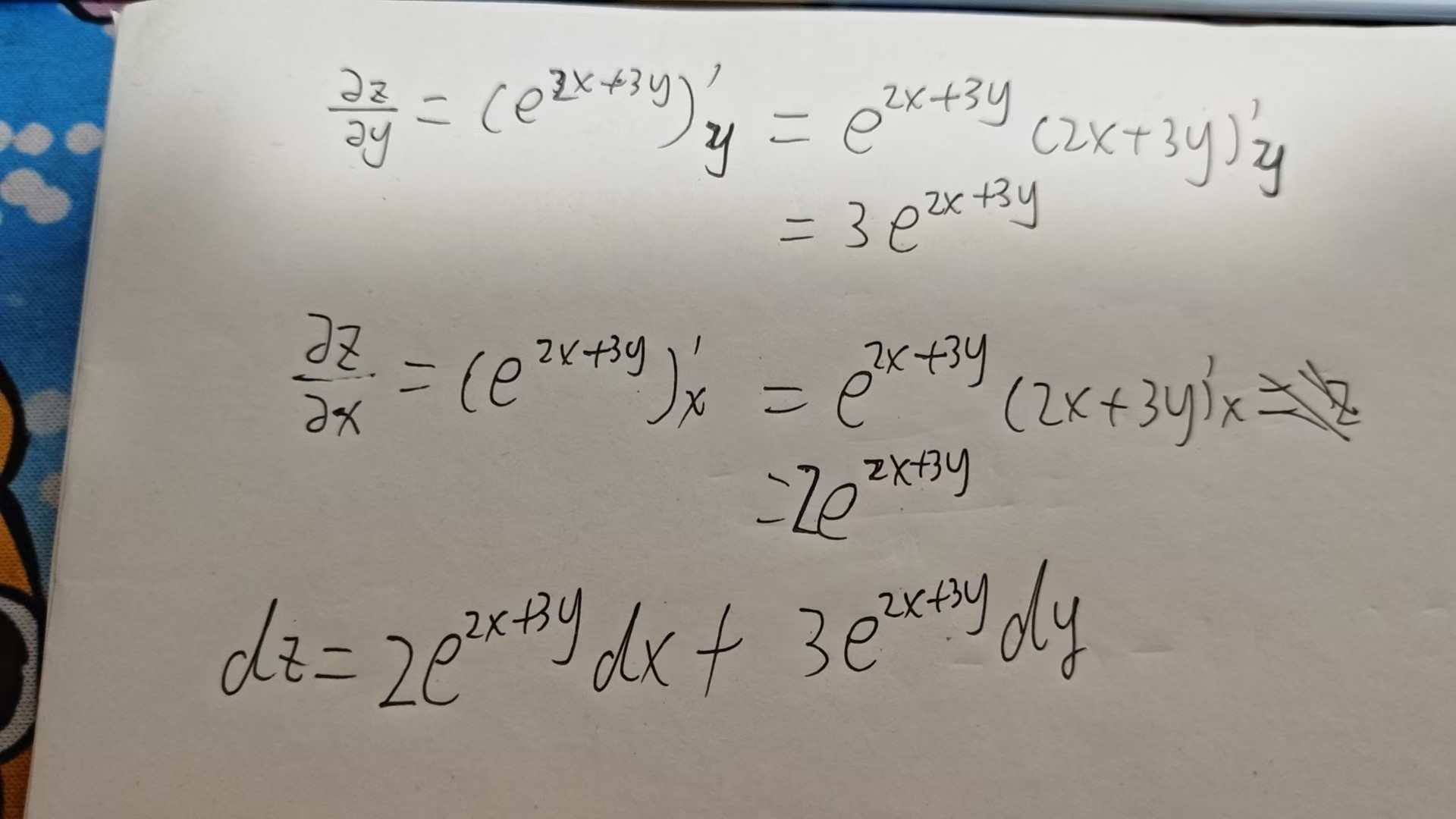
给个例题,求函数 z=f(x,y)=yx2 在 点 (1,−2) 出,当 △x=0.02 , △y=−0.01 时的全增量。
先求函数的两个偏导数得出。
dz=y2x△x−y2x2△y
将 △x=0.02 , △y=−0.01 代入,得 −0.0175。
下面是这个函数的图像。
由微分和全微分的基础知识可知,在数学中进行一些计算时,其精确度会有所丢失。
偏导数求最小值
在学习导数时,我们知道当 f′(a)=0 时,该函数取得极值,推广到多元函数中,也可以通过偏导数来求取极值。例如,对于二元函数 z=f(x,y) ,当符合下面条件时,可以取得极值:
∂x∂z=0,∂y∂z=0
这是因为此时 x、y 切线的斜率都是 0,这里就不给出推理过程了,直接记住该方法即可。
如下图是函数 z=x2+y2 的图像,求当 x、y 为何值时,函数取得最小值。
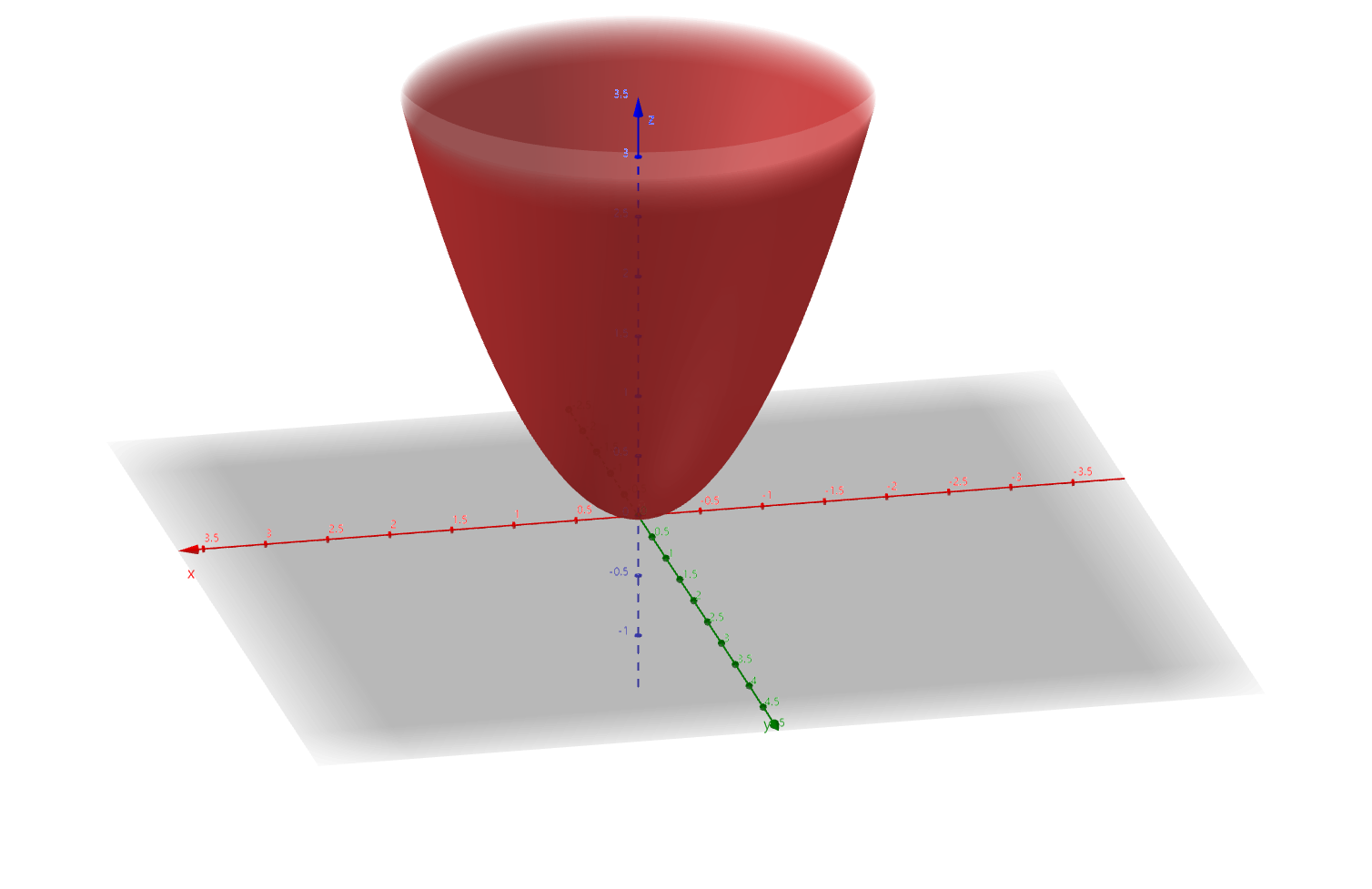
很明显,当 x、y 都是 0 的时候,函数取得最小值,但是我们要通过数学来推到,不能只凭图像得出结论。
先求偏导数:
∂x∂z=2x∂y∂z=2y
可知,当 x=0,y=0 时,两个偏导数结果都是 0,所以 z=f(x,y) 只有在 (0,0) 处有唯一的极值。
因为 z=x2+y2≥0 ,所以可知, z=f(0,0) 时取得最小值。
当 x、y 的斜率越来越接近 0 时,可以看到曲面切线越来越光滑。
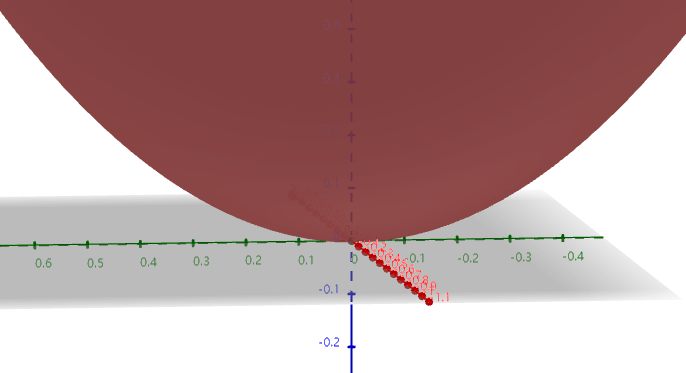
拉格朗日乘数法
有一个二元函数 z=(x,y) ,以及附加条件 φ(x,y)=0 ,而拉格朗日乘数法就是用来求解这种有条件限制的多元函数极值问题。
公式如下:
F(x,y,λ)=f(x,y)+λφ(x,y)
其中 λ 是一个参数,也是我们要求解的值,求出 λ 后可以求得 z 的最小值。
首先将上面的公式进行偏导数求导,并且求出为 0 的条件:
Fx′(x,y,λ)=fx′(x,y)+λφx′(x,y)=0
Fy′(x,y,λ)=fy′(x,y)+λφy′(x,y)=0
Fλ′(x,y,λ)=φ(x,y)=0
通过上述方程求出 x、y、λ 之后,代入 f(x,y) 求得极值。
例题 a+b=1 ,求 a1+b4 的最小值。
首先,二元函数是 z=f(a,b)=a1+b4。
约束条件 φ(a,b)=a+b−1=0 。
所以:
F(a,b,λ)=f(a,b)+λφ(a,b)=a1+b4+λ(a+b−1)
现在开始求偏导数。
Fa′(a,b,λ)=fa′(a,b)+λφa′(a,b)=−a21+λ=0(1)
Fb′(a,b,λ)=fb′(a,b)+λφb′(a,b)=−b24+λ=0(2)
Fλ′(a,b,λ)=φ(a,b)=a+b−1=0(3)
由 (1)、(2)、(3) 解得:
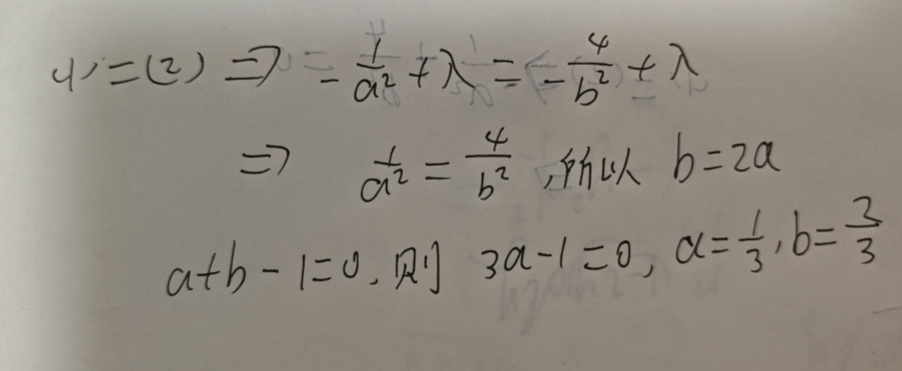
代入 z=f(a,b)=a1+b4 ,求得 zmin=f(31,32)=9 ,所以最小值是 9。
1.6. 梯度
在本节中,我们将学习深度学习里面重点之一的梯度下降法,梯度下降法要学习的知识比较多,本文的内容基本都是为梯度下降法做铺垫。
百度百科:方向导数本质上研究的是函数在某点处沿某特定方向上的变化率问题,梯度反映的是空间变量变化趋势的最大值和方向。
方向导数
前面提到导数,在一元函数中, y=f(x) ,导数是反映了其在某点的变化率,而在 z=f(x,y) 中,两个偏导数 ∂x∂z 、 ∂y∂z 则是反映函数沿着平行于 x 轴 、y 轴方向上的变化率。偏导数反映的是往某个轴方向的变化率,而方向导数则是某个方向的变化率,而不是某个轴方向。
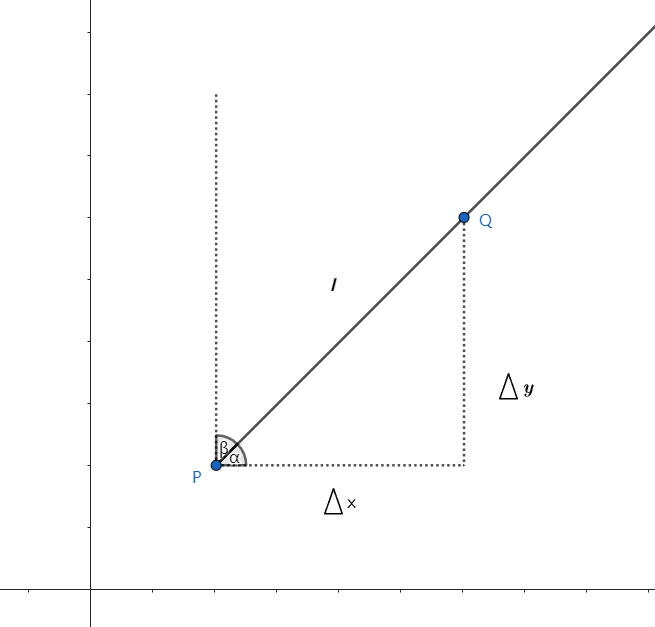
如上图所示,设 l 是一条有 P(x,y) 引出来的一条射线, Q(x+△x,y+△y) 是 l 上的一点,设 ρ 是 P 、 Q 两点之间的距离,则:
ρ△z
该公式反映函数在了 P 、 Q 两点之间沿着 l 方向的平均变化率,如果当 Q 趋近于 P 时,极限存在,则该极限值称为点 P 沿方向 l 的方向导数。
由于:
△x=ρcosα,△y=ρcosβ
所以方向导数可以表示为:
∂l∂z==∂x∂z△x+∂y∂z△y=∂x∂zcosα+∂y∂zcosβ
如果使用 i 、 j 表示 x、y 上的分量,也可以表示为:
∂l∂z=∂x∂zi+∂y∂zj
如果我们使用向量表示,也可以表示为:
(∂x∂z,∂y∂z)
梯度
梯度是指函数的值在哪个方向增长最快,后面学习的梯度下降则是相反的,是函数值下降最快的方向。
在空间中的一点,当点 P 固定时,方向 l 变化时,函数的方向导数 ∂l∂u 也随之变化,说明了对于固定的点,函数在不同方向上的变化率也有所不同。那么对于点 P ,在什么方向上可以使得函数的变化率达到最大?这里需要引入梯度的概念。
下图是一个半球。
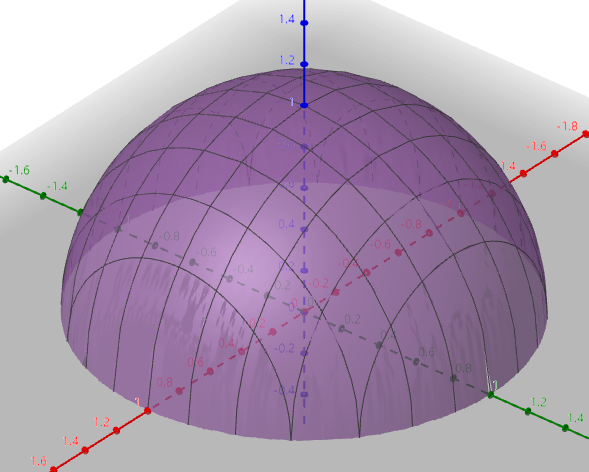
问,怎么给定任意一点,怎么最快地达到顶部?很明显,垂直往上走,可以最快到底顶部,但是对于实际中凹凸不平的图像来说,是不能直接得出结论的,不过我们这里可以先简单讨论。
就像上面的图形,给定可微的二元函数 z=f(x,y) ,有一点 (x0,y0) ,这个点可以往各种方向走,每个方向的方向导数都不一样,现在假设有个方向可以让方向导数最大,这个就是梯度 gradf(x0,y0)。
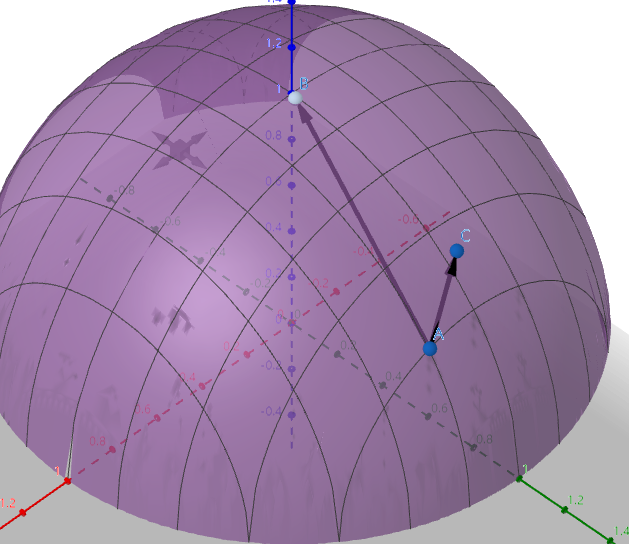
如图所示, A(x0,y0) 往 B 方向可以让 A 最快到达顶点,也就是变化率最大。而 A 有各种方向,其中一个是往 C 走。
往 B 方向的方向导数最大,就是梯度 gradf(x0,y0) 。由图所示,从 A 开始的任意一个方向导数,跟 AB 都有一个夹角,因为是在空间,所以这个夹角表示起来有点麻烦,就是各个方向的余弦值,我们也是有向量表示: ne=(cosα,cosβ) ,那么方向导数、梯度的关系:
∂l∂z=gradf(x0,y0)⋅ne
∂l∂z=∂x∂zcosα+∂y∂zcosβ=gradf(x0,y0)⋅ne
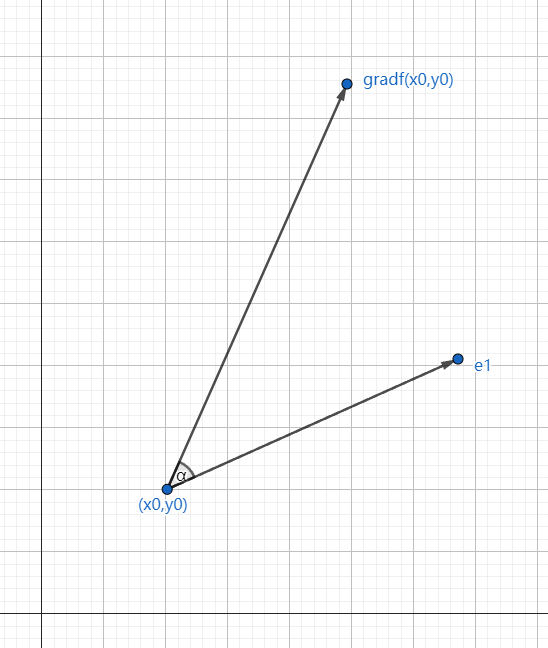
如下图所示,当 α=0 时, gradf(x0,y0) 和 e1 重合, 由于 cosα=1 ,所以方向导数也达到最大值 ∣gradf(x0,y0)∣ 。也就是,沿着梯度方向的方向导数可以达到最大值。
所以:
gradf(x0,y0)=∂x∂zcosα+∂y∂zcosβ=∂x∂zi+∂y∂zj=(∂x∂z,∂y∂z)
例题,求函数 z=ln(x2+y2) 的梯度。
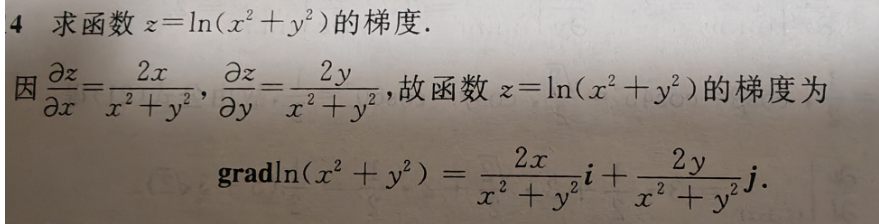
来源:《高等数学工本》陈兆斗。
再来一道实际意义的题目。

来源:《高等数学工本》陈兆斗。
使用 C# 求解该题,得:
var x = torch.tensor(2.0, requires_grad: true);
var y = torch.tensor(1.0, requires_grad: true);
var z = torch.tensor(-1.0, requires_grad: true);
var u = x.pow(2) + y.pow(2) + z.pow(2);
u.backward();
var ux = x.grad;
var uy = y.grad;
var uz = z.grad;
Console.WriteLine("gradu(2,1,-1) = {"{"}{ux.ToScalar().ToDouble()},{uy.ToScalar().ToDouble()},{uz.ToScalar().ToDouble()} {"}"}");
gradu(2,1,-1) = {4,2,-2 }
梯度下降法的基本公式
建议读者阅读这篇文章,这样很容易理解什么是梯度下降:https://www.zhihu.com/question/434600945
前面提到,梯度是向上最快,那么梯度下降就是向下最快,跟梯度相反就是最快咯。
梯度下降法是神经网络的武器,相信大家在了解深度学习时,也最常出现梯度下降的相关知识,所以本小节将讲解梯度下降法的一些基础知识。
在偏导数求最小值一节中,我们学习到最小值需要满足以下条件:
∂x∂z=0,∂y∂z=0
如果可以直接通过偏导数计算出梯度,那么问题就简单了,直接计算出最小值,都是对于实际场景要计算出来是比较可能的,尤其在神经网络里面。所以大佬们使用另一种方法来求出最小值的近似值,叫梯度下降法。
画出一个三维图像如图所示:
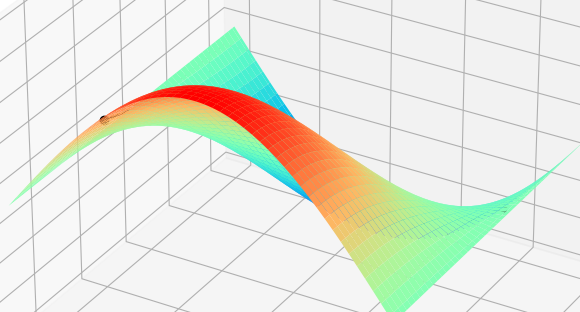
假如你正在最高位置,将你蒙上眼睛后,你要从最上面移动到最底的位置,每次只能移动一个格。
我们要最快下降到底部,肯定要选择最徒的路径,但是因为蒙着眼睛,无法跳过一个格知道后面的格的位置,所以只能先从附近的格对比后,找到最徒的格,然后再走下一步。但是不可能所有的格都走一次吧?可以先选几个格,然后判断哪个格最徒,接着走下一步,然后再选几个格,再走下一步。
在前面学习梯度时,我们知道:
∂l∂z=∂x∂z△x+∂y∂z△y
即:
△z=∂x∂z△x+∂y∂z△y
如果我们把这个公式当作两个向量的内积,可以得出:
△z=(∂x∂z,∂y∂z)⋅(△x,△y)
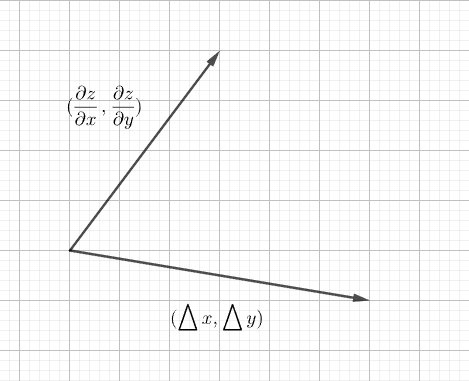
当以下向量方向相反时, △z 取得最小值。
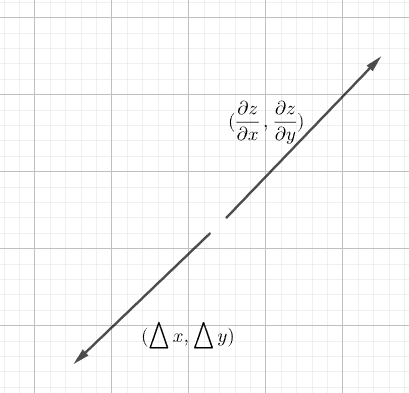
让我们回顾向量知识,当两个向量的方向相反时,向量内积取得最小值。由于:
a⋅b=∣a∣∣b∣cosθ
所以向量 b 满足:
b=−ka
(k 为正的常数)
设 b=(△x,△y) , a=(∂x∂z,∂y∂z) , k=η ,所以:
(△x,△y)=−η(∂x∂z,∂y∂z)
(η 为正的微小常数)。
这个公式称为二变量函数的梯度下降法基本公式,如果推广到三个变量以上:
(△x,△x2,...,△xn)=−η(∂x1∂x,∂x2∂z,...,,∂xn∂z)
(η 为正的微小常数)
前面学习方向导数和梯度的时候,我们知道沿着梯度的方向导数最大,此时梯度是 (∂x∂z,∂y∂z) ,也就是向上是最徒的。
由于 (△x,△y) 是跟梯度相反的向量,所以向下是下降最快的,所以这就是梯度下降法求使得下降最快的向量。
回顾使用偏导数求最小值 z=x2+y2 ,求:当 x 从 1 变成 1+△x 、y 从 2 变到 2+△y 时,求出使得这个函数减小最快的向量 (△x,△y) 。
首先求出偏导数:
∂x∂z=2x∂y∂z=2y
根据梯度下降法的基本公式得出:
(△x,△y)=−η(2x,2y)
(η 为正的微小常数)
由题意当 x=1、y=2 时,得出:
(△x,△y)=−η(2,4)
(\eta为正的微小常数)
在本小节中,还有一个 η 没有讲解,它是一个非常小的正数,就像下山问题中的一个格,即移动的步长。在使用计算机进行计算时,需要确定一个合适的 η 值, η 值过小或过大都会导致一些问题,而在神经网络中, η 称为学习率,没有明确的方法求出 η 值,只能通过反复实验来寻找合适的值。
哈密算子 ▽
当梯度下降法推广到多个变量时,下面的公式会显示非常复杂:
(△x,△x2,...,△xn)=−η(∂x1∂x,∂x2∂z,...,∂xn∂z)
(η 为正的微小常数)
所以数学上经常使用 ▽ 符号简化公式。
▽f=(∂x1∂x,∂x2∂z,...,∂xn∂z)
替换到梯度下降法公式就是:
(△x,△x2,...,△xn)=−η▽f(η为正的微小常数)
梯度下降法求最小值的近似值
在学习梯度下降法的基本公式时,提到了 η ,那么继续回顾 z=x2+y2 的问题,我们如果设置学习率 η=0.1 ,那么根据梯度下降法,我们怎么使用这个算法求最小值呢?假设初始点是 (3,2) ,根据梯度:
(△x,△y)=−0.1(2x,2y)(η为正的微小常数)△x=−0.2x△y=−0.2y
代入 (3,2) ,得:
| 第几次运算 |
当前位置 |
当前位置 |
梯度 |
梯度 |
位移向量 |
位移向量 |
函数值 |
| i |
x |
y |
∂z/∂x |
∂z/∂y |
∆x |
∆y |
z |
| 0 |
3.00 |
2.00 |
6.00 |
4.00 |
-0.60 |
-0.40 |
13.00 |
所以,点 (3.00,2.00) 已经移动到 (2.40,1.60) ,所以:
| 第几次运算 |
当前位置 |
当前位置 |
梯度 |
梯度 |
位移向量 |
位移向量 |
函数值 |
| i |
x |
y |
∂z/∂x |
∂z/∂y |
∆x |
∆y |
z |
| 0 |
3.00 |
2.00 |
6.00 |
4.00 |
-0.60 |
-0.40 |
13.00 |
| 1 |
2.40 |
1.60 |
|
|
|
|
重新计算梯度等步骤,得出:
| 第几次运算 |
当前位置 |
当前位置 |
梯度 |
梯度 |
位移向量 |
位移向量 |
函数值 |
| i |
x |
y |
∂z/∂x |
∂z/∂y |
∆x |
∆y |
z |
| 0 |
3.00 |
2.00 |
6.00 |
4.00 |
-0.60 |
-0.40 |
13.00 |
| 1 |
2.40 |
1.60 |
4.80 |
3.20 |
-0.48 |
-0.32 |
8.32 |
反复执行运算,最终可以算出最小值,如果步骤越少,那么下降的速度最快。
在 Pytorch 中,梯度下降算法有很多种,这里不再赘述,读者感兴趣可以参考这篇文章:https://zhuanlan.zhihu.com/p/619988672